Rozkład normalny Excel

Rozkład normalny jest jednym z najważniejszych i najczęściej stosowanych rozkładów prawdopodobieństwa w statystyce i analizie danych. Jest to rozkład ciągły, który opisuje wiele zjawisk w naturze i społeczeństwie, takich jak wzrost ludzi, wyniki testów, wyniki sportowe, czy też wartości rynkowe. Excel to popularny program do analizy danych, który umożliwia analizę rozkładu normalnego. W tym artykule omówimy, jak korzystać z funkcji Excela do obliczania wartości rozkładu normalnego i wykorzystywania go w analizie danych.

SPIS TREŚCI

Czym dokładnie jest rozkład normalny w Excelu i nie tylko?

Definicja

Funkcja rozkładu normalnego, znana również jako funkcja Gaussa, to funkcja matematyczna, która opisuje rozkład prawdopodobieństwa zmiennej losowej o wartościach ciągłych. Jest to rozkład symetryczny wokół średniej, gdzie większość wartości znajduje się blisko tej wartości średniej, a im dalej od niej, tym mniejsza jest liczba wartości. Rozkład normalny jest opisany przez dwa parametry: średnią (μ) i odchylenie standardowe (σ). Funkcja rozkładu normalnego może być wykorzystana do obliczenia wartości prawdopodobieństwa dla określonej wartości w tym rozkładzie.

Parametry funkcji rozkładu normalnego

W Excelu funkcja rozkładu normalnego nazywa się ROZKŁAD.NORMALNY. Funkcja ta oblicza wartość rozkładu normalnego dla określonej wartości x, średniej μ i odchylenia standardowego σ. Wzór na rozkład normalny w excelu wygląda następująco:

=ROZKŁAD.NORMALNY(x,μ,σ,kumulatywny)

Parametry funkcji to:

• x – wartość, dla której obliczamy wartość rozkładu normalnego,
• μ – średnia
• σ – odchylenie standardowe
• kumulatywny – opcjonalny parametr, który określa, czy funkcja ma obliczać wartość kumulatywną rozkładu normalnego. Domyślnie przyjmuje wartość TRUE.

Poniżej znajduje się wizualizacja, jak wygląda funkcja rozkładu normalnego w Excelu

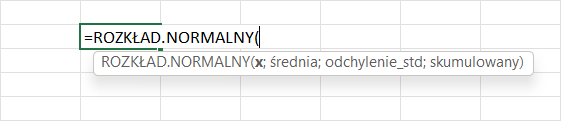
Przykład użycia Funkcji rozkładu normalnego

Przykładowo, jeśli chcemy obliczyć wartość rozkładu normalnego dla x=1, μ=0 i σ=1, użyjemy formuły:

=ROZKŁAD.NORMALNY(1,0,1,TRUE)

Funkcja zwróci wartość 0,8413, co oznacza, że wartość rozkładu normalnego dla x=1 wynosi 0,8413.

Użycie rozkładu normalnego za pomocą Excela w praktyce

1. Utwórz arkusz kalkulacyjny i wprowadź dane w kolumnie dotyczące wydatków firmy na artykuły biurowe w poszczególnych miesiącach. A (od A1 do A10). Przykładowo, wprowadź dane jak na poniższym obrazku.

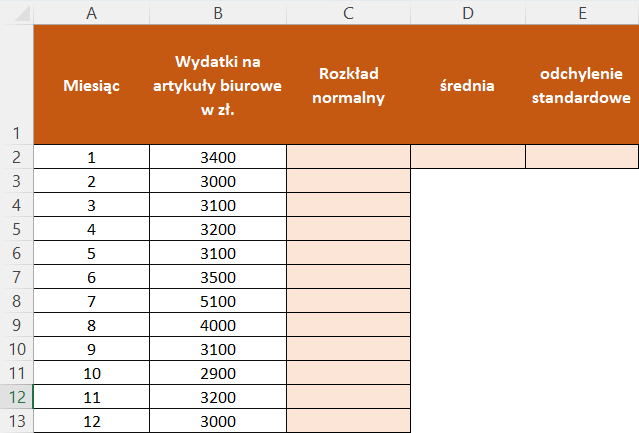
2. Oblicz średnią oraz odchylenie standardowe. By to zrobić wprowadź formułę =ŚREDNIA(B2:B13) która obliczy średnią danych oraz =ODCH.STAND.POPUL(B2:B13). 

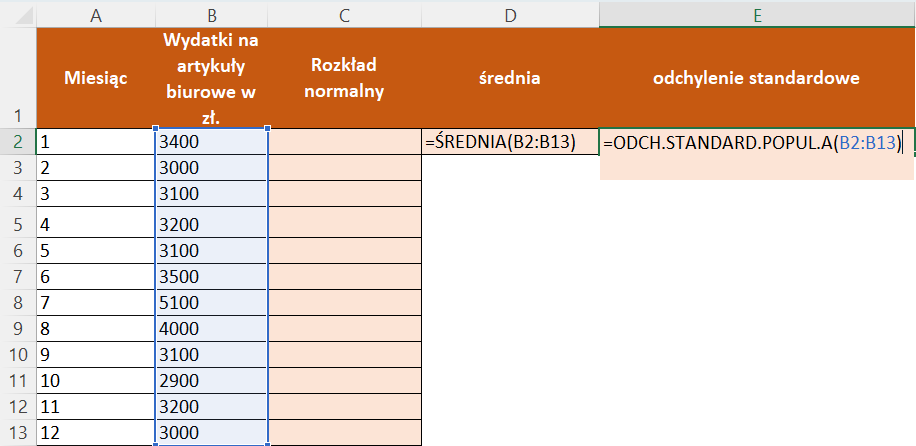
3. Wprowadź w komórce C2 formułę =ROZKŁAD.NORMALNY(B2;$D$2;$E$2;PRAWDA) bazującą na wynikach średniej oraz odchylenia standardowego i wciśnij klawisz Enter. Wykorzystaliśmy funkcję ROZKŁAD.NORMALNY, która zwraca wartość dystrybuanty standardowego rozkładu normalnego dla określonej wartości x, średniej, odchylenia standardowego i wartości logicznej określającej czy obliczenia mają być dokładne czy przybliżone.

=ROZKŁAD.NORMALNY(B2;$D$2;$E$2;PRAWDA)

4. Skopiuj formułę z komórki C2 do pozostałych komórek w kolumnie

5. W kolumnie C znajdują się wartości dystrybuanty standardowego rozkładu normalnego dla każdej wartości w kolumnie B. Poniżej znajduje się obraz finalnej wersji.

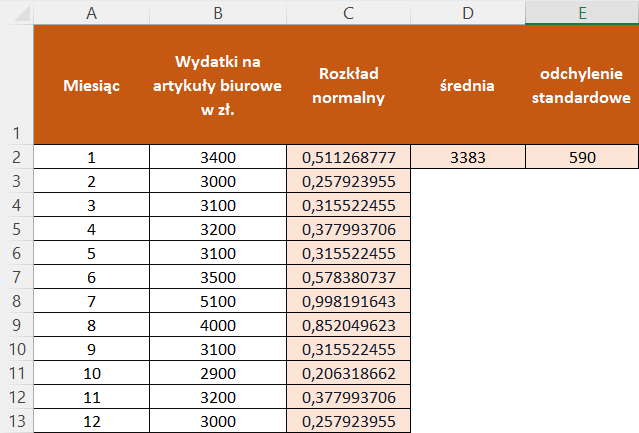
Możesz teraz wykorzystać te wartości do analizy i interpretacji rozkładu danych, np. obliczając prawdopodobieństwo, że wartość z kolumny B będzie mniejsza lub większa od określonej wartości.

W jakich dziedzinach rozkład normalny ma zastosowanie?

Jednym z najważniejszych zastosowań funkcji rozkładu normalnego jest modelowanie i prognozowanie zjawisk losowych. Na przykład, w finansach, rozkład normalny może być używany do modelowania zmienności rynkowej, co pozwala inwestorom na ocenę ryzyka i prognozowanie przyszłych trendów. W naukach społecznych, rozkład normalny jest stosowany do modelowania różnych zjawisk, takich jak poziomy dochodów, wzrost populacji czy wyniki testów psychometrycznych.

Innym zastosowaniem funkcji rozkładu normalnego jest obliczanie przedziałów ufności dla estymatorów statystycznych, takich jak średnia, odchylenie standardowe czy korelacja. Przedziały ufności to przedziały wartości, które zawierają prawdziwą wartość parametru z pewnym określonym prawdopodobieństwem. Przykładowo, przedział ufności dla średniej może pomóc w określeniu, z jaką dokładnością średnia próbki reprezentuje średnią populacji.

Rozkład normalny jest również często wykorzystywany w testach statystycznych, takich jak testy istotności lub testy hipotez. Testy te umożliwiają badanie, czy wyniki uzyskane z próby różnią się istotnie od teoretycznego modelu lub wartości oczekiwanych.