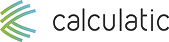Excel odchylenie standardowe
Odchylenie standardowe to jedna z najczęściej stosowanych miar zmienności w analizie danych. W Excelu możemy łatwo obliczyć odchylenie standardowe za pomocą funkcji.
SPIS TREŚCI
Definicja odchylenia standardowego
Na początku warto przybliżyć czym w ogóle jest odchylenie standardowe. Jest to miara zmienności określająca, jak bardzo wyniki pomiarów lub obserwacji różnią się od średniej. Można ją traktować jako miarę rozrzutu wyników wokół wartości średniej. Odchylenie standardowe jest wykorzystywane w wielu dziedzinach, w tym w statystyce, ekonomii, naukach przyrodniczych oraz w kontroli jakości produktów.
Rodzaje odchylenia standardowego
Za pomocą Excela możemy użyć dwóch głównych funkcji obliczających odchylenie standardowe
- ODCH.STANDARD.POPUL.A – służy do obliczenia odchylenia standardowego całej populacji
- ODCH.STANDARD.PRÓBKI – służy do obliczenia odchylenia standardowego próbki populacji
Wybór funkcji, której użyjecie zależy od sytuacji w której będzie używana. Funkcje ODCH.STANDARD.POPUL.A należy użyć gdy posiadamy dane całej grupy (populacji), natomiast gdy chcemy interpretować wyniki całej grupy posiadając dane jedynie części z nich, należy użyć funkcji ODCH.STANDARD.PRÓBKI
Przykładowe sytuacje w których należy użyć poszczególnych funkcji w celu obliczenia odchylenia standardowego w Excelu:
| ODCH.STANDARD.POPUL.A | ODCH.STANDARD.PRÓBKI |
| Wydatków na artykuły biurowe w poszczególnych miesiącach | Wzrostu wśród Polaków |
| Wyników kolokwium studentów danego kierunku | Kompetencji pracowniczych na podstawie testu przeprowadzonym na 40% pracowników |
| Pensji pracowników danej firmy | Wynagrodzenia sprzedawców w województwie Dolnośląskim |
Składnia funkcji
Parametry funkcji to liczby, dla których chcemy obliczyć odchylenie standardowe populacji. Funkcja może przyjąć od jednej do 255 argumentów. Parametry te mogą być liczbami, referencjami do komórek lub tablicami.
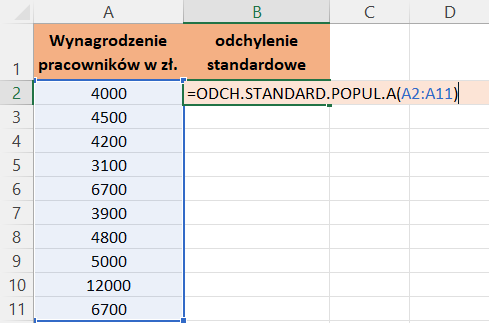
Przykładowo, jeżeli chcemy obliczyć odchylenie standardowe dla wynagrodzenia pracowników danego działu wpiszemy formułę =ODCH.STANDARD.POPUL.A a w polu argumentów wpisujemy adresy komórek lub zaznaczamy zakres komórek, tak jak na obrazie poniżej
Obliczyć odchylenie standardowe możemy również z kilku różnych zbiorów. W tym celu wystarczy kolejno zaznaczać następne zbiory przytrzymując klawisz „ctrl”, tak jak w poniższym obrazie
Jak interpretować otrzymane wyniki?
Wynik odchylenia standardowego informuje nas o tym, jak bardzo nasze wyniki pomiarów lub obserwacji różnią się od wartości średniej. Im większe jest odchylenie standardowe, tym większy jest rozrzut wyników wokół wartości średniej. Z kolei mniejsze odchylenie standardowe oznacza, że wyniki pomiarów lub obserwacji są bardziej skupione wokół wartości średniej.
Kiedy odchylenie standardowe przydaje się w praktyce
Funkcja ODCH.STANDARD.POPUL.A jest narzędziem, które pomaga analizować dane i podejmować decyzje biznesowe. Zastosowanie tej funkcji w praktyce pozwala na dokładne oszacowanie, jak bardzo wartości w populacji różnią się od średniej wartości. Dlatego warto zapoznać się z jej zastosowaniem i umiejętnie korzystać z niej w swojej pracy.
Dziedziny w których odchylenie standardowe znajduje zastosowanie
Funkcja ta znajduje zastosowanie w wielu dziedzinach, w tym w analizie biznesowej, naukowej i finansowej. Na przykład, w branży finansowej, funkcja ODCH.STANDARD.POPUL.A może być stosowana do analizy wahań cen akcji w określonym okresie czasu. W analizie biznesowej, funkcja ta może pomóc w ocenie, jak bardzo wyniki finansowe różnią się od średniej wartości.
Wyniki uzyskane za pomocą funkcji ODCH.STANDARD.POPUL.A pozwalają na lepsze zrozumienie rozkładu danych i podejmowanie decyzji biznesowych na podstawie bardziej precyzyjnych oszacowań. Wynik odchylenia standardowego populacji można również porównać z innymi wartościami, takimi jak średnia, minimum i maksimum, aby uzyskać bardziej kompletny obraz danych.
Garść przykładów, jak zastosować funkcję odchylenie standardowe w Excelu
- W analizie sprzedaży: funkcja ta może pomóc w ocenie, jak bardzo wyniki sprzedażowe różnią się od średniej wartości i pomóc w identyfikacji obszarów, w których potrzebne są zmiany lub ulepszenia.
- W badaniach naukowych: funkcja ta może być używana do obliczania rozrzutu wyników badań, co pozwala na dokładniejsze oszacowanie, jak dokładnie dane wyniki odzwierciedlają badany proces.
- W analizie finansowej: funkcja ta może pomóc w ocenie ryzyka inwestycyjnego, ponieważ wysokie odchylenie standardowe oznacza większe ryzyko inwestycyjne.
- W analizie zasobów ludzkich: funkcja ta może pomóc w ocenie wydajności pracowników i identyfikacji obszarów, w których potrzebne są ulepszenia lub dodatkowe szkolenia.